Detecting critical cut-in-scenarios

Egal, ob bei hoch entwickelten Fahrerassistenzsystemen oder Robotertaxis, Sicherheit spielt eine entscheidende Rolle. Dabei gibt es zwei Aspekte zu beachten: Die funktionale Sicherheit (FuSi) [1] sorgt dafür, dass Fehler im System selbst vermieden werden, während die „Safety Of The Intended Functionality“ (SOTIF) [2] darauf achtet, dass alle Situationen gemeistert werden können, für die die Funktion entwickelt wurde.

Doch wie wird das Ziel der SOTIF – diese Sicherheit der Sollfunktion [3] – überhaupt erreicht? Alle möglichen Szenarien durchzuprobieren ist nicht machbar, weil deren Zahl in der Regel zu groß, wenn nicht sogar unendlich ist. Da man aber davon ausgeht, dass die meisten Situationen keine Probleme bereiten, kann den Fokus auf die Suche nach kritischen Szenarien verschoben werden, in denen die Fahrfunktion versagt oder zumindest große Schwierigkeiten bekommt. Für Testszenarien gilt somit der Grundsatz „Qualität geht vor Quantität“: Die Anzahl der real oder in der Simulation gefahrenen Kilometer ist damit gar nicht so wichtig.

Die gezielte Suche nach kritischen Testfällen stößt seit einiger Zeit auf immer mehr Interesse. So hat eine Gruppe von Forschern der University of Michigan ein Verfahren entwickelt, mit dem das Verhalten anderer Verkehrsteilnehmer so optimiert wird, dass das getestete System Schwierigkeiten hat, damit zurechtzukommen [4]. Eine andere Gruppe von Wissenschaftlern aus Schweden hat mit einem genetischen Suchverfahren eine Vielzahl an Szenarien gefunden, bei denen Baidu Apollo in der Simulation versagt hat [5].

Wir arbeiten daran, die Szenariensuche weiter zu verbessern, indem wir Kausalität und maschinelles Lernen verbinden. In der Regel prädiziert und detektiert das klassische Machine Learning (ML) ausschließlich auf Basis von Korrelationen. Die Kausalität fehlt dabei. Ein ML-System kann dann zwar immer noch gute Ergebnisse liefern, es „weiß“ aber nicht, wie oder warum diese zustande kommen.

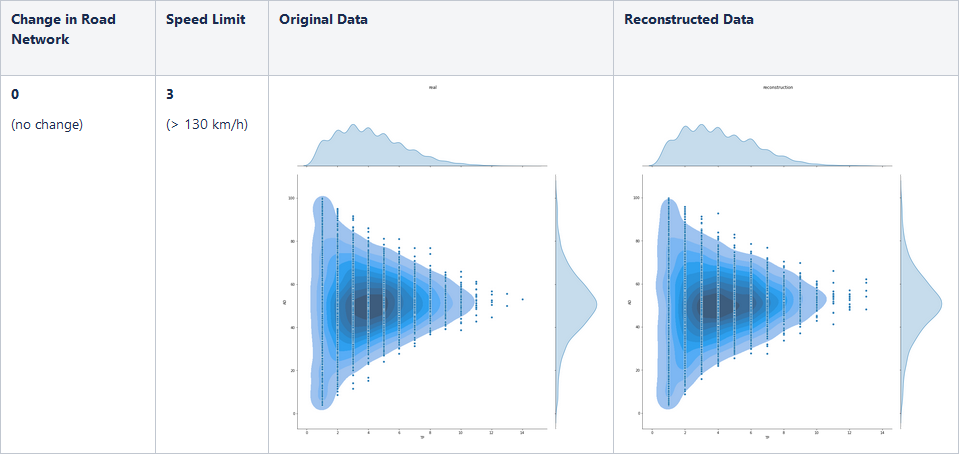
Mit der Beachtung kausaler Zusammenhänge schaffen wir Abhilfe. Wir ordnen dabei zunächst die verschiedenen Variablen und Einflussfaktoren, die wir quantitativ erfassen können, in einem kausalen Graphen an. In diesem führt eine gerichtete Kante stets von einer Ursache zur Wirkung. Wichtig sind darüber hinaus noch die Mechanismen, um in Abhängigkeit von den Ursache-Variablen die Werte der Wirkungsvariablen zu berechnen. Die Mechanismen lassen sich meist in einen deterministischen Term und ein probabilistisches Rauschen aufteilen. Beides kann mit Daten wie beim klassischen maschinellen Lernen ermittelt werden.

Ein Vorteil dieser Methoden besteht darin, dass man die Auswirkungen des Setzens eines bestimmten Variablenwerts einer Ursache auf deren Wirkungen zuverlässiger ermitteln kann. Auch sogenannte kontrafaktische Fragestellungen lassen sich damit beantworten. Gemeint sind Fragen nach der Art: Was wäre gewesen, wenn? Oder etwas ausführlicher: Wie wäre in einem ganz bestimmten Fall die Wirkung gewesen, hätte die Ursache einen anderen Wert gehabt?

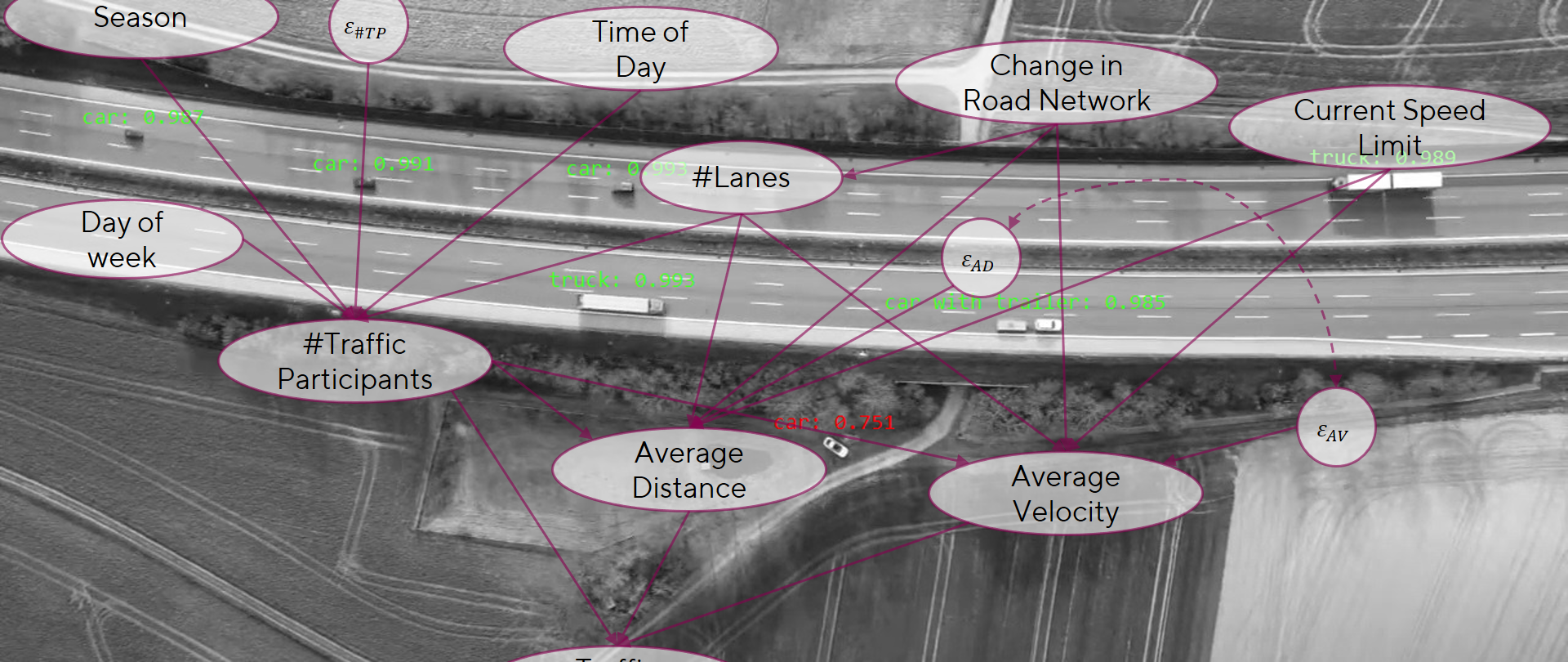
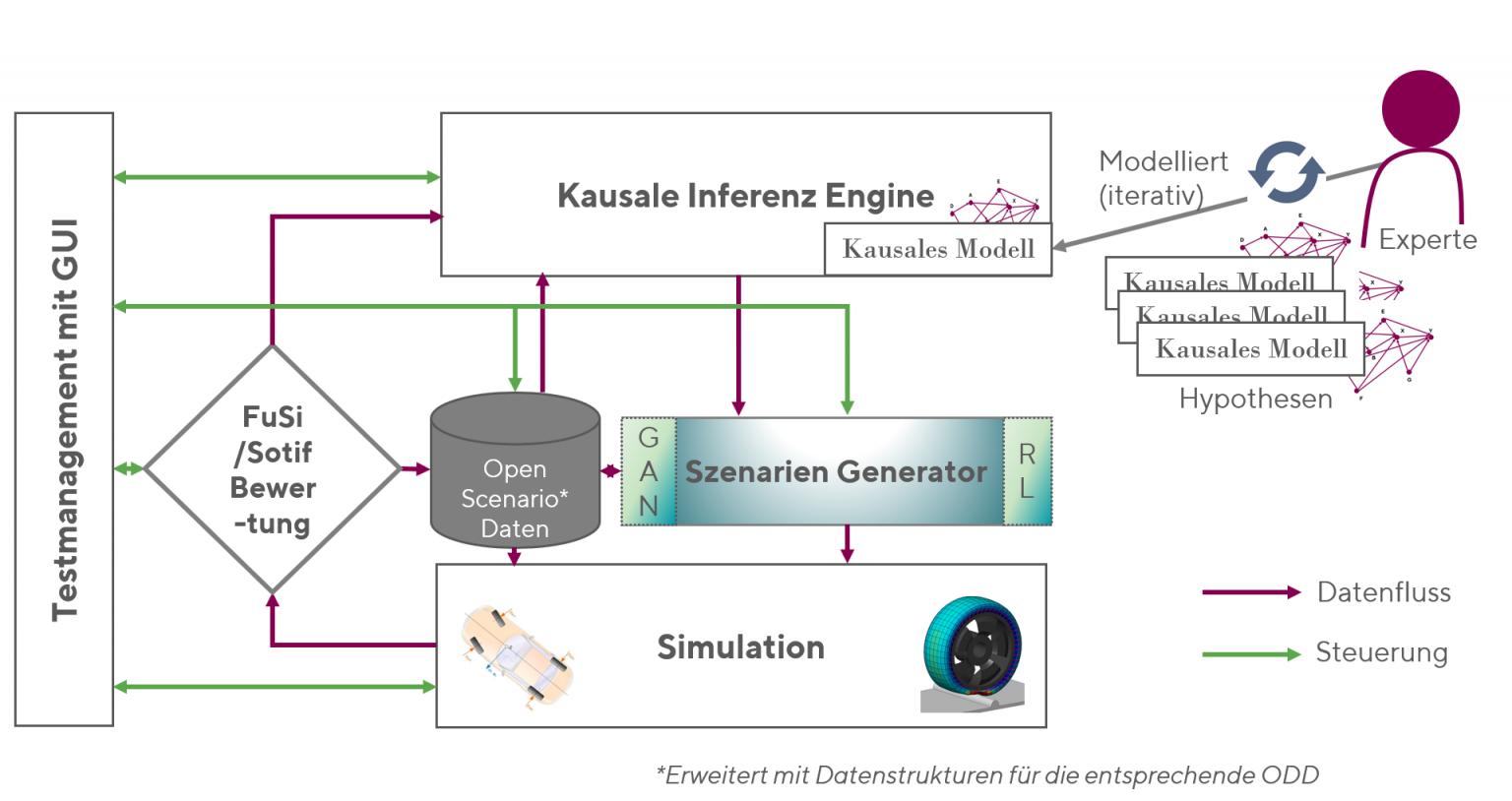
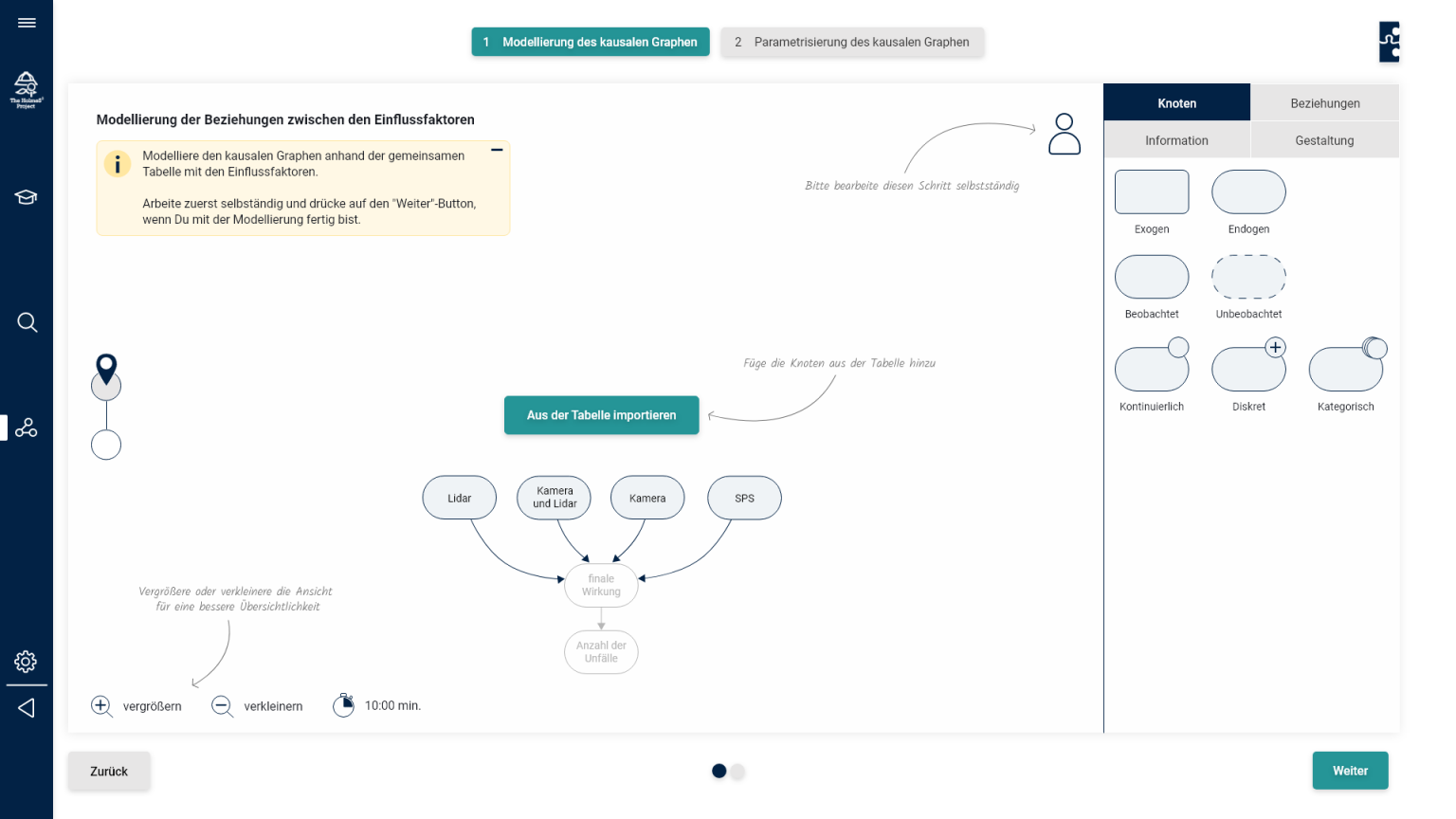
Unser Ziel ist es, mit der Hilfe von Fachexperten und Verkehrsdatensätzen ein kausales Modell aufzubauen, das uns bei der Suche nach kritischen Einscher-Szenarien hilft. Es wird uns dabei helfen, den Suchraum der Szenarien besser einzuschränken und um die sogenannten Corner Cases so leichter zu finden.

[1] ISO 21448

[2] ISO 26262

[3] https://de.wikipedia.org/wiki/SOTIF

[4] https://arxiv.org/abs/2102.03483

[5] https://arxiv.org/abs/2109.07960